Método Fridrich modificado (parte 4)
2. Colocación de esquinas de la primera capa
3. Colocación de aristas de la segunda capa
4. Preparación de la última capa
5. Orientación de la última capa
Cuadro 9: Algoritmos de la orientación de la última capa
Caso
Figura
Algoritmos
Llegados a este punto, hay que permutar las aristas, esto es, cambiarlas de posición. Hay que fijarse en cuántas aristas están bien posicionadas (como ejemplo, en la Figura 9, la arista roja y amarilla está en el lugar correcto).
Hay que mover la capa superior, para ver cuántas aristas bien posicionadas se pueden conseguir. Hay tres casos:
6.1. Ninguna arista bien posicionada
Hay que fijarse en cómo están intercambiadas las aristas (lo estarán por parejas), dando lugar a dos posibilidades (detalladas en el Cuadro 10):
Cuadro 10: Permutación de aristas - 0 aristas bien posicionadas
Caso
Figura
Descripción
Algoritmo
1
Visto desde arriba, las aristas están intercambiadas en cruz.
M2A - M2A2 - M2A - M2
M2U - M2U2 - M2U - M2
2
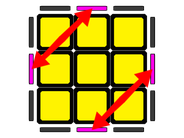
Visto desde arriba, las aristas están intercambiadas en diagonal.
DT'D'T - FD'F - T'D'TD - F2 - A
RB'R'B - FR'F - B'R'BR - F2 - U
6.2. Una arista bien posicionada
Se gira la capa superior (o todo el cubo, para visualizar mejor la situación), hasta que la arista coincidente esté enfrente nuestro. Llegados a este punto, hay dos posibilidades (ver Cuadro 11):
Cuadro 11: Permutación de aristas - 1 arista bien posicionadas
Caso
Figura
Descripción
Algoritmo
1
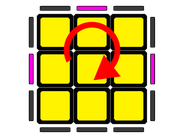
Visto desde arriba, las aristas deben permutar en sentido horario.
D'A - D'A' - D'A' - D'A - DAD2
R'U - R'U' - R'U' - R'U - RUR2
2
Visto desde arriba, las aristas deben permutar en sentido antihorario.
D2A'D' - A'D - AD - AD - A'D
R2U'R' - U'R - UR - UR - U'R
6.3 Dos aristas bien posicionadas
En esta ocasión, sólo hay una posibilidad (Cuadro 12):
Cuadro 12: Permutación de aristas - 2 aristas bien posicionadas
Caso
Figura
Descripción
Algoritmo
1
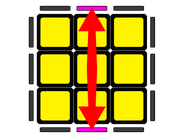
Visto desde arriba, las aristas bien posicionadas deben quedar a derecha e izquierda. Para ello se gira la capa superior del cubo (o todo el cubo, para visualizarlo mejor).
DT'D'T - FD'F - T'D'TD - F2
RB'R'B - FR'F - B'R'BR - F2