IBERO RUBIK

Índice de contenidos:

1. Introducción

2. Centros

3. Aristas

4. Resolución del cubo

3. Aristas

Una vez resuelto los centros del cubo es necesario agrupar las aristas de un mismo color en un solo triplete de aristas, de tal forma que obtengamos un total de 12 aristas compuesta por 3 piezas cada una (debidamente orientadas). Para ello tendremos que aplicar un movimiento que nos permitirá juntar dos aristas, por lo tanto tendremos que aplicar dos veces dicho movimiento para completar un triplete de aristas. En esta fase de la resolución del cubo debemos preocuparnos de los casos de paridad, que serán solventadas bien aplicando una serie de precauciones a la hora de juntar las aristas o bien aplicando un movimiento extra.

En esta fase procederemos a juntar las piezas que formaran un triplete de aristas compuesto por tres piezas. El movimiento que presentamos las agrupa de dos en dos, de tal forma que en primer lugar juntaremos la arista central con una lateral, y posteriormente agruparemos la otra arista lateral con las dos aristas ya juntadas. Para ello debemos poner una arista central cualquiera en la intersección de la cara F con la cara U. Esta arista central será nuestra referencia para mover la primera arista lateral, la cual estará situada en la intersección de la cara B con la cara U (el lateral en

el que están situados influirá en el movimiento a utilizar). En el Cuadro 5 se muestra primero cómo juntar las pieza central e izquierda de la arista y después cómo hacer lo propio con las piezas central y derecha.

Cuadro 5: Movimientos básicos para agrupar las piezas central e izquierda o las aristas central y derecha de la arista

Una vez que hemos juntado la arista central con una arista lateral procedemos a unir la otra arista lateral, aplicando los mismos movimientos (ver Cuadro 6):

Cuadro 6: Movimientos básicos para agrupar las tres piezas de la arista

Puede darse la circunstancia de que las aristas que vayamos a emparejar no estén correctamente orientadas (al contrario de lo que ocurre en los Cuadros 5 y 6) dando como resultado un caso de paridad, es decir, un triplete de aristas juntas pero mal orientadas (ver Figura 5).

Para solucionarlo tenemos dos opciones: seguir juntando aristas y reorientarlas aplicando un algoritmo extra al final, o bien recolocando las aristas de tal forma que estén correctamente orientadas a la hora de aplicar los movimientos del Cuadro 5. Para cambiar la orientación de una arista es necesario aplicar el siguiente movimiento, teniendo en cuenta que además de cambiar la orientación, cambia la posición (ver Cuadro 7).

Cuadro 7: Movimientos básicos para cambiar la orientación (y posición) de la pieza de una arista

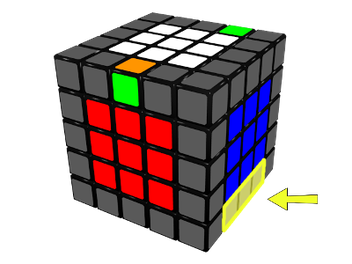
Cuando apliquemos los movimientos del Cuadro 5, tenemos que tener presente que cuando juntamos dos aristas necesariamente se deshacen otras dos. Debemos elegir que arista queremos “sacrificar”, de tal forma que sepamos en todo momento que aristas juntamos y que aristas separamos. Por ejemplo, si queremos juntar la arista central con la arista de la izquierda, al aplicar el movimiento 5a desharemos la arista que esté colocada en la intersección de la cara D con la cara L (ver Figura 6), mientras que si queremos juntar la arista central con la arista de la derecha aplicando el movimiento 5b desharemos la arista que esté colocada en la intersección de la cara D con la cara R (ver Figura 7).

Todo lo anterior nos vale para juntar todos los tripletes de aristas excepto las dos últimas. Para poder juntar los dos últimos tripletes de aristas debemos aplicar un movimiento extra. Para realizar este movimiento es fundamental colocar correctamente las aristas que vayamos a mover. Para cada arista, el par de piezas unidas que vayamos a juntar con una tercera debe estar en la intersección de la cara F con la cara U (la pieza lateral puede estar tanto a la izquierda como a la derecha). La pieza que vayamos a juntar con las otras dos deber estar enfrente de las piezas ya emparejadas, en la intersección de la cara B con la cara U. Es fundamental que la pieza a mover esté enfrente del par de piezas unidas, de tal forma que si el par de piezas está compuesto por la pieza central y la pieza izquierda, la que vayamos a colocar debe estar en frente de la arista izquierda, y si el par de piezas está compuesto por la pieza central y la derecha, la que vayamos a colocar debe estar enfrente de la pieza derecha (ver Cuadro 8). Para poder seguir correctamente esta regla será necesario aplicar los movimientos del Cuadro 6 tanto en el par de piezas juntado como en la pieza a juntar.

Cuadro 8: Movimientos para emparejar las dos últimas aristas. Triplete de piezas de la arista bien orientadas.

Puede darse la circunstancia de que las aristas que vayamos a colocar no estén debidamente orientadas, por lo que después de aplicar los movimientos del Cuadro 7 nos da como resultado un triplete de aristas unidas pero mal orientadas (ver Cuadro 9). Posteriormente debemos aplicar un movimiento extra para poder orientar correctamente el triplete de aristas.

Cuadro 9: Movimientos para emparejar las dos últimas aristas. Triplete de piezas de la arista mal orientadas.

Con los pasos anteriores podemos tener resultas las aristas del cubo, pero como se ha mencionado previamente, por lo general tendremos algún triplete de aristas mal orientadas. Para solucionarlo podemos aplicar un solo movimiento para orientarlas adecuadamente (algo más largo y complicado que los anteriores). Este movimiento se presenta en el Cuadro 10.

Cuadro 10: Movimiento para orientar adecuadamente los tripletes de aristas.

4.  Resolución del cubo como un 3x3x3

Una vez que tengamos completados los centros y los doce tripletes de aristas, únicamente nos queda resolverlo como si se tratase de un cubo de 3x3x3. Para ello debemos asumir lo siguiente (ver Cuadro 11):

Cuadro 11: Equivalencias entre los cubos de 5x5x5 y de 3x3x3